How medication dosage miscalculations impact both patients and pharmacies
Medication errors are a persistent and pervasive problem in the U.S. The latest estimates suggest that each year in the U.S. alone, 7,000 to 9,000 people die as a result of a medication error, costing more than $40 billion in associated healthcare costs.
In their 2007 landmark report, the Institute of Medicine reported that at least 1.5 million preventable medication errors harm patients in the United States each year. Since then, technology has enhanced our ability to detect many types of medication errors, but human errors, especially those involving calculations, continue to be a problem.
Medication dosage miscalculations are unfortunately common and often go unnoticed. Prescriptions can be filled incorrectly by simply missing one crucial piece of information, like weight, or applying a proportion calculation incorrectly.
Download our infographic for a visual you can hang in your pharmacy or classroom and read on for three scenarios that can help you illustrate the impact of a miscalculation.
Incorrect calculation based on weight
A retail pharmacy receives a prescription for a nine-month old weighing 13 lbs., 5 oz. for amoxicillin that says, “Give 333 mg Amoxicillin suspension every 12 hours for 7 days.” As it reads, the prescription is for 666 mg per day. For amoxicillin, the usual dose for children over three months old is 25 mg/kg per day, given in evenly-divided doses every 12 hours.
The pharmacy technician goes on to fill the prescription, unaware that the 9-month-old patient weighs 13 lbs., 5 oz. (13.3125 lbs.).
There are two errors in this calculation, resulting in a dose far higher than the dosing guidelines with respect to the weight of a child.
- The dosage was calculated based on weight in pounds, not kilograms
- The dosage should be split evenly every 12 hours but was instead prescribed to receive the full amount twice daily.
Here is the correct calculation: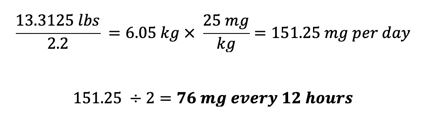
The incorrect calculation led to a dosage over four times higher than the intended dose. This is an example where one error can be further compounded and magnified by subsequent errors.
There are several cases where incorrect dosages for pediatric patients have resulted in serious injury or death. Swapping pounds and kilograms, or even just having the wrong weight to begin with, can make a serious impact on a patient.
Incorrect calculations for IV drug in a critical situation
A hospital’s pharmacy receives a request from a nurse to “double concentrate” a dopamine IV. The standard dopamine IV concentration is 400 mg per 250 mL 5% dextrose in water (D5W). The hospital has multiple bag sizes for D5W and the technician chooses a 100 mL bag. Dopamine is available in 10 mL vials containing 80 mg/mL solution. The technician needs to calculate how much dopamine solution is needed to prepare the 100 mL “double concentrate” dopamine IV.
The technician uses dimensional analysis to calculate the correct amount of dopamine, but doesn’t track her units of measure, causing her to misplace a number, resulting in calculating a lower concentration dopamine IV than the standard concentration.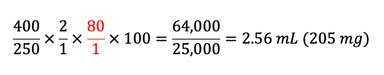
Here is the correct calculation: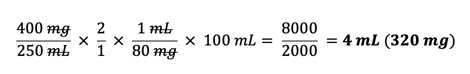
Because dopamine’s effects are heavily dose-dependent, small differences in concentration may mean the difference between increasing urine output or increasing cardiac output. In an emergency situation, it is critically important that the correct dose be administered to bring about the desired effect.
Incorrect calculation impacts revenue
Aside from the medical implications, pharmacy miscalculations can potentially have a highly negative impact to revenue.
A pharmacy receives a prescription for Sucralfate suspension with the following directions:
Take 1 g Sucralfate suspension q6h x14 days then take 1 g q12h to prevent ulcer recurrence
Qty: QS 30 days
Refills: 5
Sucralfate (Carafate®) suspension has an available concentration of 1,000 mg/10 mL. Sucralfate treats existing ulcers by forming a sugar complex over the ulcer to protect the area from further injury due to stomach acid, bile, and pepsin; to prevent ulcers, sucralfate acts as an anion buffer to reduce the amount of free acid in the stomach.
The prescription is written for a higher dose initially, intended to treat an existing duodenal ulcer, and then for a lower maintenance dose thereafter to prevent the ulcer from recurring. The technician calculates that the quantity needed (QS) per 30 days of treatment as:
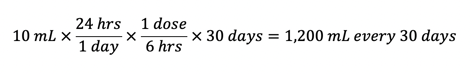
The patient’s Medicare Part D plan pays for the medication and every refill every 30 days for six months. A few months after discontinuing the medication, the patient’s part D plan performed an audit and determined that the calculated volume was incorrect, and therefore they were billed incorrectly. As a result, the plan recouped the total amount paid to the pharmacy for all six fills. Over the six-month period, the pharmacy dispensed a total of 7,200 mL or roughly 15 pints.
The initial amount filled should have been: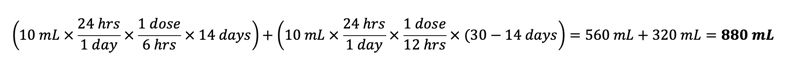
The amount filled for each refill should have been:
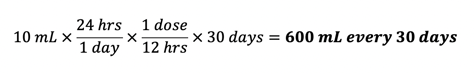The total volume dispensed over six months should have been:
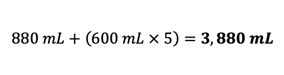The total difference between volume dispensed, and what the correct volume should have been:
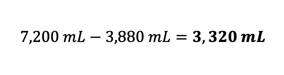Because the pharmacy billed the prescription incorrectly and received reimbursement for nearly double the volume of the prescribed amount, the part D plan charged back all funds paid for the prescription. With a listed Average Wholesale Price (AWP) of $251 per 14 oz bottle, and a reimbursement rate of AWP – 18% + $1.60 dispensing fee, the total revenue loss to the pharmacy comes out to be: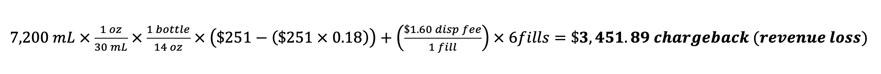
Setting a foundation for correct calculations in the pharmacy
Complicated dosage calculations clearly pose a challenge to both safety of patients and pharmacy operations. Technicians in training often struggle with the complicated nature of pharmacy math. At the same time, trainers and educators find it difficult to teach these mathematical concepts in a way that resonates with all students because they’ve often only relied on one method themselves.
Luckily, there are three different ways to accurately calculate dosages, giving technicians and those training them more tools to find success:
| 1. Desired over have: |  |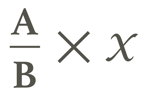
| 2. Dimensional analysis: |  |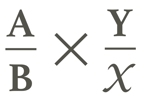
| 3. Ratio/proportion: |  |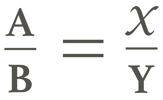
As you consider how you train your current and future technicians to be reliably accurate, it’s critical to address any anxiety that exists around math, in general. Building confidence is key and providing multiple tools to validate their learning and ability will lead to improvements in performance.
What tools do you use to ease the challenges of teaching pharmacy math?
